数据结构原理
二叉树
相关概念
满二叉树:所有的度(就是节点)都是 2,就称为满二叉树。
完全二叉树:从左向右边,的节点没有间断,即为完全二叉树。(有右节点,肯定有左节点,有左节点,不一定有右节点)
非完全二叉树:有间断了,就是非完全二叉树。
性质
第i层节点:2(i-1)
层次为k的二叉树,最多有 $2^{k-1}$个节点
对任何一颗二叉树,如果其叶子节点数为 n0,度为 2 的节点数为 n2, 则有 n0 = n2 + 1
哈希表
定义
散列表(Hash table,也叫哈希表),是根据键(Key)而直接访问在内存存储位置的数据结构。也就是说,它通过计算一个关于键值的函数,将所需查询的数据映射到表中一个位置来访问记录,这加快了查找速度。这个映射函数称做散列函数,存放记录的数组称做散列表。
本质
本质就是数组,具体实现中,分别可以采用:
- 数组+链表
- 数组+二叉树
后一种结构主要用于解决哈希冲突
哈希内核
哈希函数/散列函数
大白话散列函数:
例如,查找人名比较快的方法是按照首字母排序,再查找。
对应到哈希表中,直接拿到当前首字母(值地址)的方法就是散列函数。
- 常见的哈希函数
一个哈希函数的好不好,取决于以下三点
- 哈希函数的定义域必须包括需要存储的全部关键码,而如果哈希表允许有m个地址时,其值域必须在0 到m-1之间
- 哈希函数计算出来的地址能均匀分布在整个空间中
- 哈希函数应该比较简单
eg:除留余数法、直接定制法、平方取中法
哈希冲突
解决哈希冲突主要有两个方案:闭散列 和 开散列
闭散列
也叫开放定址法,当发生哈希冲突时,如果哈希表未被装满,说明在哈希表中必然还有空位置,那 么可以把key存放到冲突位置中的“下一个” 空位置中去
闭散列中主要处理方法有
线性探测和二次探测线性探测:下一个空的位置;伪删除;当前数据达到负载因子这个阈值时,就需要将当前表进行扩容;
二次探测:通过当前位置的哈希冲突次数的平方查找新的位置;
开散列
链地址法
哈希表中存储的是链表的头结点。具有相同的哈希地址会存放在同一链表中,每个链表中的元素都具有相同的哈希地址。
LSH
References
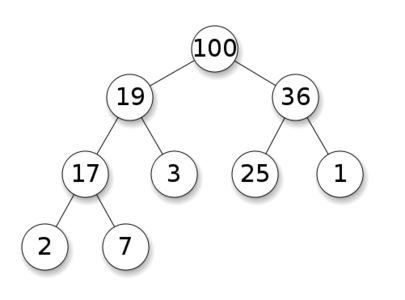
最小堆与最大堆
堆树的定义
堆树的定义如下:
(1)堆树是一颗完全二叉树;
(2)堆树中某个节点的值总是不大于或不小于其孩子节点的值;
(3)堆树中每个节点的子树都是堆树。
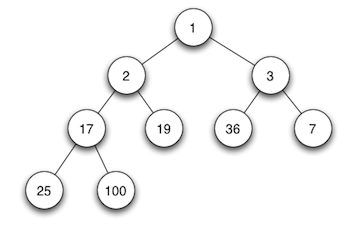
当父节点的键值总是大于或等于任何一个子节点的键值时为最大堆。 当父节点的键值总是小于或等于任何一个子节点的键值时为最小堆。
堆树操作
构造最大堆
思路:将每个叶子节点视为一个堆,再将每个叶子节点与其父节点一起构造成包含一个更多节点的堆
实现:首先需要找到最后一个节点的父节点,从这个节点开始构造最大堆;直到该节点前面所有分支节点都处理完毕插入节点
思路:在堆的最后添加一个节点,然后沿着堆树上升。删除节点
思路:将堆树的最后的节点提到根结点,然后删除最大值,然后再把新的根节点放到合适的位置。
堆排序
相当于是堆树操作中的删除节点的操作。
1、创建一个最大(小)堆H;
2、把堆首和堆尾元素互换;
3、把堆的大小减1,重新构造一个最大(小)堆;
4、重复步骤2、3,直到堆的大小减少为1。