大模型外推窗口扩充技术

Posted on In

本文主要围绕扩充上下文窗口相关工作尽心介绍。

随着大规模模型的不断提出，怎么高效扩充上下文窗口是一个关键的问题，如果能够基于前者的一些工作再微调，不用再从头训练扩充LLM的本身的参数是一个比较需要的一个方案。

基于RoPE的Position Interpolation

https://arxiv.org/abs/2306.15595

  • 代码实现：https://github.com/ymcui/Chinese-LLaMA-Alpaca/pull/705
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    import transformers
    def pi_forward(self, x, seq_len=None):
        if seq_len > self.max_seq_len_cached: # seq_len > 2048
            print(f"Perform position interpolation for length {seq_len}")
            t = torch.arange(seq_len, device=x.device, dtype=self.inv_freq.dtype)
            scale = self.max_seq_len_cached / seq_len
            t *= scale
            freqs = torch.einsum("i,j->ij", t, self.inv_freq)
            emb = torch.cat((freqs, freqs), dim=-1).to(x.device)
            cos_cached = emb.cos()[None, None, :, :]
            sin_cached = emb.sin()[None, None, :, :]
            return (
                cos_cached[:, :, :seq_len, ...].to(dtype=x.dtype),
                sin_cached[:, :, :seq_len, ...].to(dtype=x.dtype)
            )
        return (
            self.cos_cached[:, :, :seq_len, ...].to(dtype=x.dtype),
            self.sin_cached[:, :, :seq_len, ...].to(dtype=x.dtype)
        )
    transformers.models.llama.modeling_llama.LlamaRotaryEmbedding.forward = pi_forward

RoPE

绝对位置编码优点：实现简单、可提前计算好，速度快。外推性相对较差。

相对位置编码优点：相对位置信息对模型要更加有效，外推性更好，处理长文本能力更强。

RoPE通过绝对位置编码的方式实现相对位置编码，综合两者的优点。公式化就是：$\langle\boldsymbol{f}(\boldsymbol{q}, m), \boldsymbol{f}(\boldsymbol{k}, n)\rangle = g(\boldsymbol{q},\boldsymbol{k},m-n)$

具体方法

借助复数实现将绝对位置编码和相对位置编码结合，通过复数的指数形式就可以实现如上的效果。由于复数乘法的几何意义对应着向量的旋转，因此才成为旋转式位置编码
$$
\begin{equation}
\boldsymbol{f}(\boldsymbol{q}, m) =\begin{pmatrix}\cos m\theta & -\sin m\theta\ \sin m\theta & \cos m\theta\end{pmatrix} \begin{pmatrix}q_0 \ q_1\end{pmatrix}\end{equation}
$$

image-20230719233344737

image-20230719233432878

通过这种编码方式就能够在计算注意力的同时自动获得相对位置信息，且为了避免算力浪费可以直接采用矩阵乘法实现RoPE的计算。另外，这边的$\theta_i=10000^{-\frac{2i}{d}}$,是类似于transformer三角式的带远程衰减的。带了衰减之后的两两注意力得分计算就带设定了界限。

image-20230719234011066

线性场景应用

为了降低Transformer的计算量，线性attention的方案是通过只保留线性计算的部分,不再计算Softmax以此降低需要的计算量。

Scaled-Dot Attention：
$$
\begin{equation}
Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V})i = \frac{\sum\limits{j=1}^n e^{\boldsymbol{q}_i^{\top}\boldsymbol{k}_j}\boldsymbol{v}j}{\sum\limits{j=1}^n e^{\boldsymbol{q}_i^{\top}\boldsymbol{k}_j}}
\end{equation}
$$
其中的主体计算就是一般函数$sim({q}_i,{k}_j)$,为了保持其非负，直接将原有的softmax去掉是不可行的，需要换用其他的函数计算进行替代。

由于RoPE没有对Attention矩阵本身做任何处理，因此可以直接应用到线性Attention中。

References

  1. Transformer升级之路：2、博采众长的旋转式位置编码

PI方法

直接压缩绝对位置m，将原有的m变成cur_len/max_len*m

Extending Context is Hard…but not Impossible

References

  1. Extending Context is Hard…but not Impossible
  2. 层次分解位置编码，让BERT可以处理超长文本

NTK

神经正切核Neural Tangent Kernel是一种核方法
直接作用于衰减$\theta$值

References

  1. NTK-Aware Scaled RoPE allows LLaMA models to have extended (8k+) context size without any fine-tuning and minimal perplexity degradation.

NBCE

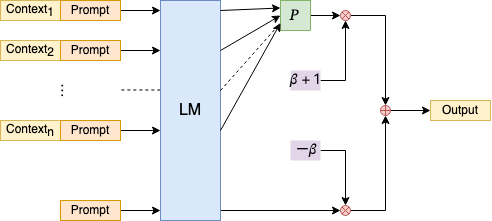
在这里插入图片描述

在输出生成结果部分，改善Random Sample的效果，将Pooling方式改为直接输出不确定性最低的那个分布