RL面经
Value-based与Policy-based
- 目标不同
vb:最大化动作价值函数
pb:最大化每个epi的总回报
基于价值与基于策略的强化学习区别:
- 价值:通过学习价值函数指导策略
- 策略:直接学习对应的策略
- ac:价值+策略
重要度采样
首先需要明确,该方法是一种普世的方法,不仅用于RL。
核心思想是通过一个已知策略的分布情况,根据采样比,进而修正得到当前未知的策略分布情况。
References
策略梯度方法
- 基本思想
最大化状态价值来更新策略函数参数,即最大化目标函数
$J(\theta) = \mathbb{E}_S[V_\pi(s)]$,其中$\theta$为策略函数的参数.具体优化过程:

- 优缺点
优点:
相对于Value Based的方法,基于策略梯度的强化学习方法的很明显的优势是它可以直接去学习Policy本身,这样学习速度会更快,并且更关键的是它可以用于连续动作空间的情况。
- 更好的收敛性
- 高维空间场景下,基于策略的方法要更高效
- 能够学习到一些随机策略
缺点:
RL环境变化往往较大,导致Value的方差要比一般的DL数据大得多,学习率的选择会直接影响到策略的好坏(学习率需要针对调整),且差异会很大。
- 方差大,受初始策略选择波动大
- 策略评估效率低
- 一般收敛到局部最优
解决办法:
TRPO与PPO,通过调整新旧策略,为新旧策略增加约束,保证策略的更新是在可控范围之内的。
- 策略梯度
选定合适的策略目标函数,对策略目标函数求梯度上升至局部最大值即可;
目标函数:
$$
J(\theta)
= \sum_{s \in \mathcal{S}} d^\pi(s) V^\pi(s)
= \sum_{s \in \mathcal{S}} d^\pi(s) \sum_{a \in \mathcal{A}} \pi_\theta(a \vert s) Q^\pi(s, a)
$$
其中$d^{\pi}(s)=\lim _{t\to \infty} P(s_t=s|s_0,\pi_\theta)$是平稳分布。
在具体更新过程中,
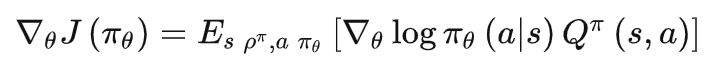
前一项控制更新方向,后一项控制更新幅度,因此就会朝着高回报的轨迹更新。
References
MC、TD与DP
Same:
References
贝尔曼方程
最优贝尔曼方程
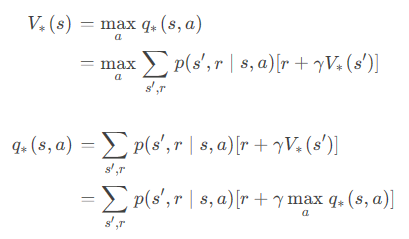
贝尔曼期望方程
