主流RL模型学习
TRPO 与 PPO
TRPO:Trust Region Policy Optimization
PPO:Proximal Policy Optimization
研究背景
策略梯度方法以及存在的缺点:策略梯度方法
TRPO相关内容
TRPO研究思路
TRPO算法尽量通过能提高状态价值的方式来更新策略。它通过在新旧策略之间增加约束,将整个参数空间的变化限制在一个小范围之内,从而避免了错误决策导致Value的崩塌,尽可能的保持快速而单调的提升。
TRPO更新与实现
- 在原有问题上增加约束项,两个策略的KL散度计算
- 引入 trust region方法去优化找到最优解
- 对当前优化问题做了一定的简化,减小计算量。具体有:
平均KL散度代替最大KL散度,对约束问题二次近似,非约束问题一次近似

PPO相关内容
PPO研究思路
TRPO中的二阶计算量还是非常大,因此基于此有了PPO算法。为了让当前策略上进行有效更新时不至于导致Value的崩溃,PPO可以看成是TRPO的一阶近似方案,其试用范围更广、计算效率更高、更容易实现。
v1:修改了KL散度的约束方式,它不再添加硬约束,而是通过在目标函数中加入KL散度的正则项的方式来处理约束问题。
v2:则删除了约束,直接使用强制剪裁的暴力方式来让$\theta$的更新保持在一定范围之内。
v2-目标函数实现:
$$
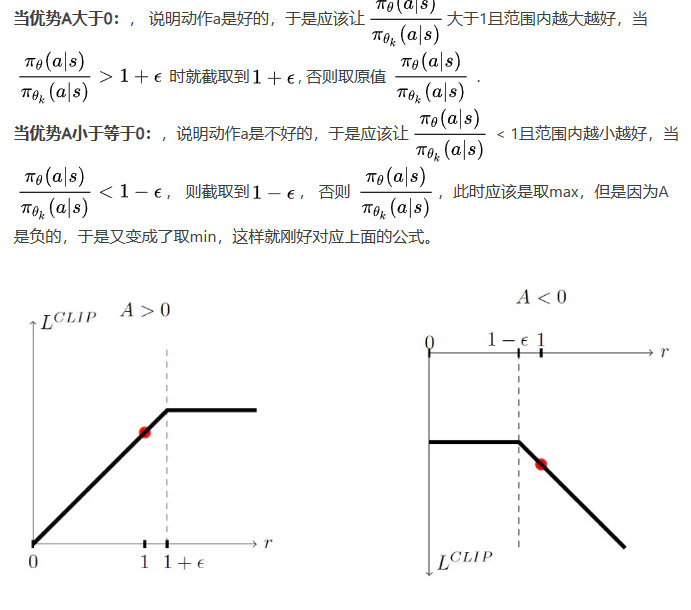
\mathcal{L}(s, a,\theta_k, \theta) = min(\frac{\pi_\theta(a|s)}{\pi_{\theta_k}(a|s)} A_{\pi_{\theta_k}}(s,a) , clip( \frac{\pi_\theta(a|s)}{\pi_{\theta_k}(a|s)}, 1-\epsilon, 1+ \epsilon) A_{\pi_{\theta_k}}(s,a))
$$
拆分讲解:
GAE:PPO的实现
GAE:generalized advantage estimator
核心思路:优势函数用类似于multi-step td去实现,获得优势函数的指数加权移动平均,这可以让优势估计更加平滑和稳定。
具体实现:
n步的Adventage的$\hat{A}t^{(n)}$估计
$$
\begin{align} \hat{A}t^{(1)} &= \delta_t^V = -V(s_t)+r_t+\gamma V(s{t+1}) \ \hat{A}t^{(2)} &= \delta_t^V + \gamma \delta{t+1}^V = -V(s_t)+r_t+ \gamma r{t+1} +\gamma^2 V(s_{t+2}) \ \hat{A}t^{(3)} &= \delta_t^V + \gamma \delta{t+1}^V + \gamma^2 \delta_{t+2}^V = -V(s_t)+r_t+ \gamma r_{t+1} + \gamma^2 r_{t+2} +\gamma^3 V(s_{t+3}) \ … \ \hat{A}t^{(k)} &= \sum^{k-1}{l=0}\gamma^l\delta_{t+l}^V = -V(s_t)+r_t+\gamma r_{t+1} + … + \gamma^{k-1}r_{t+k-1}+ \gamma^kV(s_{t+k})\ \end{align}
$$
在并不知道取哪几步优势最好的情况下,并不能确定一个最好的n,GAE则是取附近值的指数加权移动平均,加权系数$\lambda$:
$$
\hat{A}_t^{GAE(\gamma, \lambda)} = (1-\lambda)(\hat{A}_t^{(1)}+ \lambda \hat{A}_t^{(2)} + \lambda^2\hat{A}_t^{(3)}+…)
$$
当$\lambda = 0$ 时, $\hat{A}_t = \delta_t$ , 相当于one-step的TD。
当$\lambda = 1$ 时, $\hat{A}t = \sum^{\inf}{l=0}\gamma^l\delta_{t+l}$ , 相当于玩完整局才更新。
References
DPG、DDPG与TD3
DPG
DPG是确定性的策略输出,也就是说相对于随机策略输出,DPG算法面对同一个状态时将输出同一个动作,而随机策略比如说PPO,它在面对连续的动作空间时,将输出一个高斯分布的均值mu和方差sigma,并利用这个高斯分布进行采样,每一次输出的动作将不同。
在随机策略的更新中(PPO等),loss=neg_log_prob(a)*A(s,a),其中就需要得到动作a的选择概率。因此,随机策略更新可以直接采用策略梯度的目标函数进行梯度更新。
确定性策略中的动作输出代表当前的概率始终为1,所以确定性策略最大的问题在于如何去更新:
actor的目标就是采取动作a之后获取更高的后续价值,因此通过TD-target实现这一更新梯度
$loss = -Q(s,\mu_{\theta}(s))$
DDPG
DDPG主要是做了两方面改进,主要是源自于DQN的trick,Replay Buffer 和 target network
target network则是在计算loss的target部分时,为了避免Q值更新波动,采用另外的网络来计算更新的方法;其中,target网络是采用滑动更新的
TD3
TD3基于DDPG的改进主要有3方面,分别是 double Q、 Delayed update、
target policy smoothing regularization
- double Q:
在DQN中,因为DQN也有target网络,所以DQN干脆直接让target网络作为第二个Q的计算网络。可以看到这个target的Q是用目标网络来算的。
在TD3中,作者没有延续DQN使用target网络作为第二个Q的方案,而是又弄了两个网络,直接用最小的Q来作为target Q了,然后每一次更新当然也把两个Q都更新一遍。因此,相当于有6个Q网络。
- Delayed update:
延迟更新是指在更新actor网络的时候,延迟几次
- target policy smoothing regularization
作者认为相似的动作应该会有相似的值,由此提出了在目标动作的小范围拟合值的方法
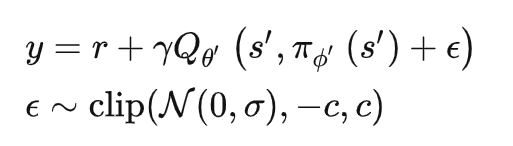
References
AC、A2C与A3C
策略梯度一般可以写为:
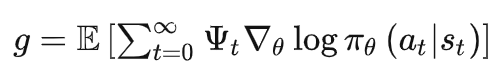
其中的$\phi_t$可以分别采用累计回报(总回报、动作开始后回报、带基线回报-回报的累计会导致方差大),值函数估计(动作值函数、优势函数、TD偏差-近似代替累计回报会导致偏差较大)
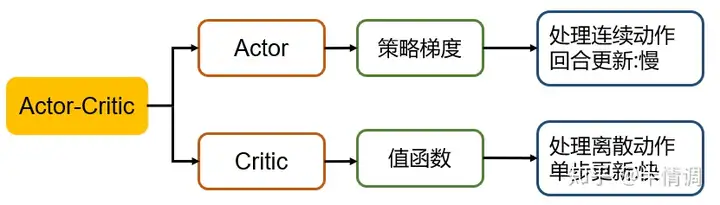
经典AC方法:actor-策略梯度,critic-值函数

- A2C
常常通过增加基线,降低模型的方差使得输出值能够标准化限制在一定范围;
值函数转换成用优势函数代替:$Q^\pi(s_t^{n},a_t^{n})-V^\pi(s_t^{n})$。评估网络只能实现一个值的评估,因此Critic变为估计状态价值V的网络,具体的更新loss:
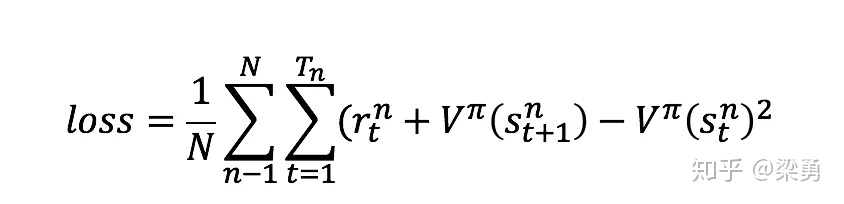
- A3C
核心思路就是异步结构,通过多个不同状态的a2c网络更新,结合多个进程实现整体的更新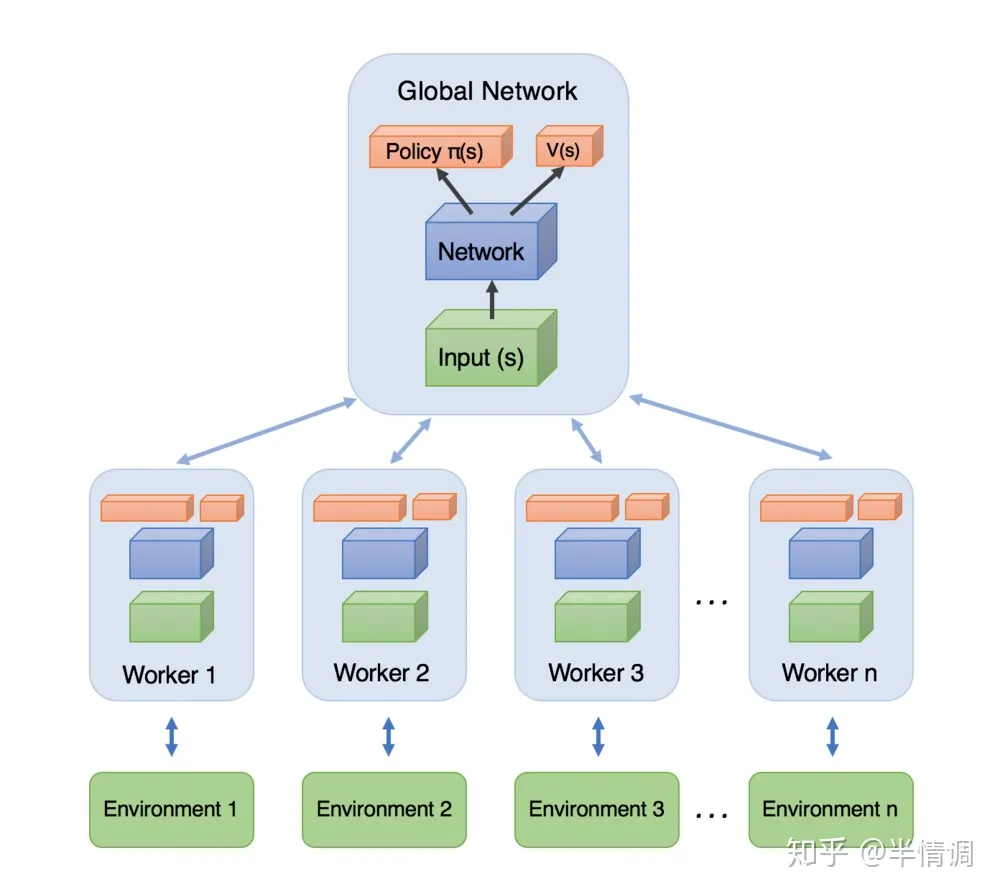
References
SAC
背景
- 随机策略PPO:重要度采样方法在应用于训练与交互policy差异过大的情况无法处理。
- 确定性策略DDPG:超参数敏感
工作
核心:最大熵算法,也采用随机分布式策略,并且是off-policy,ac算法。
实现不同:优化策略获得更高累计收益的同时也会最大化策略的熵
表现:稳定,有较强的抗干扰能力
最大熵作用:可以让策略尽可能随机,实现更充分的探索,避免策略过早落入局部最优点
熵公式:$H(P)=\underset{x \sim P}{\mathrm{E}}[-\log P(x)]$,其中x服从分布P
最大化熵强化学习:
- 目标函数:$\pi_{\text {MaxEnt }}^{*}=\arg \max {\pi} \sum{t} \mathbb{E}{\left(s{t}, a_{t}\right) \sim \rho_{\pi}}\left[r\left(s_{t}, a_{t}\right)+\alpha H\left(\pi\left(\cdot \mid s_{t}\right)\right)\right]$
$\rho_{\pi}$ 表示在策略$\pi$ 控制下,智能体(agent)会遇到的状态动作对(state-action pair)所服从的分布。 $\alpha$ 是名为温度系数的超参数,用于调整对熵值的重视程度。
Soft Value Function and Energy Based Policy
SVF:

EBP:
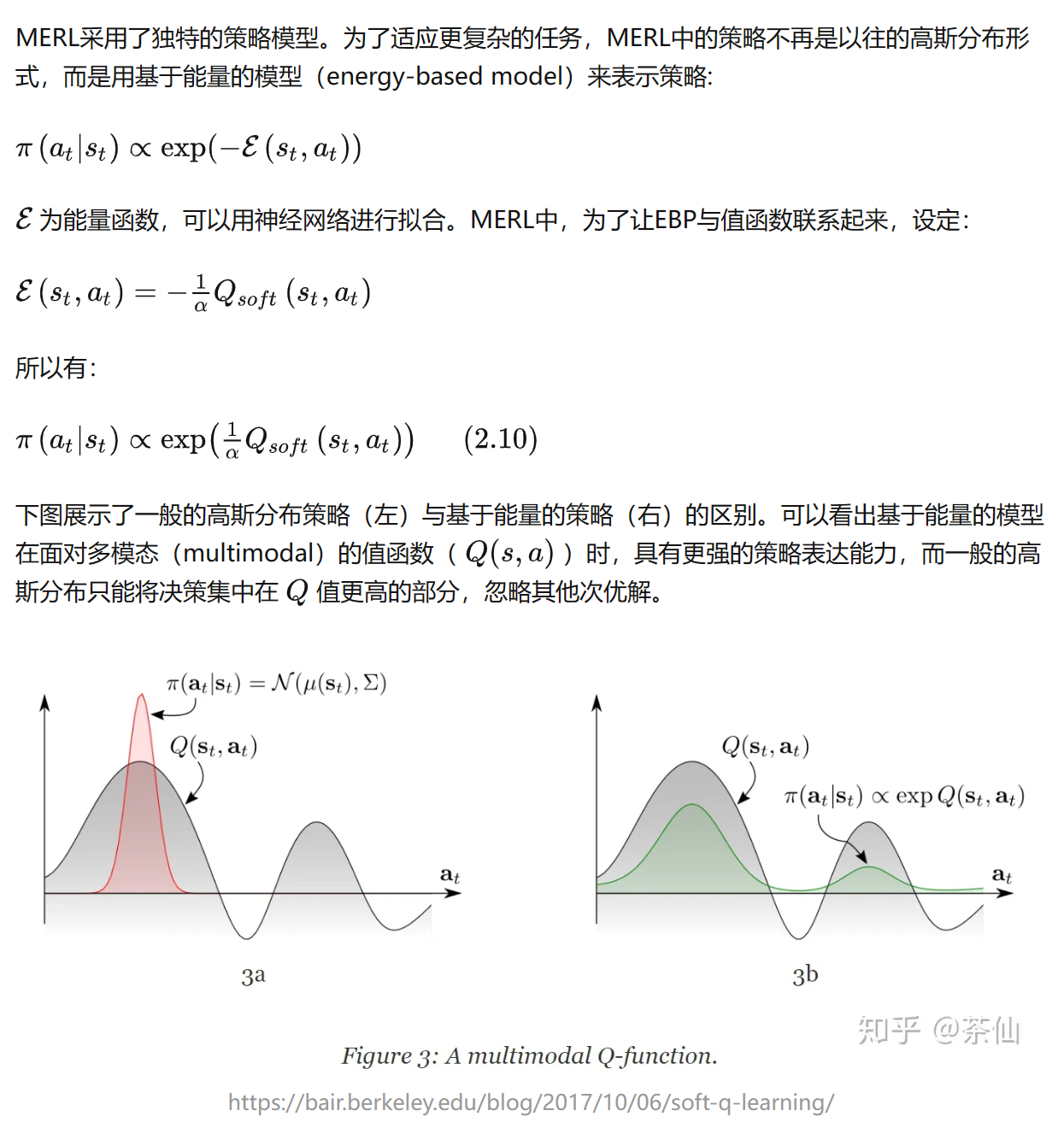
References
CQL
主要思想是在Q值基础上增加一个regularizer,学习一个保守的Q函数,作者从理论上证明了CQL可以产生一个当前策略的真实值下界,并且是可以进行策略评估和策略提升的过程。