机器学习基础

• 梯度下降算法(优化器)
  • BGD&SGD
  • Sharpness-Aware Minimization (SAM)
    • 研究背景
    • 主要工作
    • References
• 机器学习模型
  • 线性函数与非线性函数的区别
  • 逻辑回归
    • 优点
    • 代价函数
    • References
  • 朴素贝叶斯分类器
    • References
  • LSTM&GRU
    • References
• 正则化
  • L1、L2正则化
    • 数值理解
    • 分布理解
    • 直观视觉
  • References
• 损失函数
  • 交叉熵
  • 均方差损失(MSE)
  • KL散度
    • References
  • Focal loss
    • GHM
    • Refs
• HMM与CRF
  • 区别
  • 判别式模型与生成式模型
  • BiLSTM-CRF
    • CRF的引入
    • CRF矩阵的参数量
    • CRF的更新
  • References
• 常用的评价指标
  • Refs
• 归一化方法
  • 参考
• 多分类问题
• 高斯混合模型
  • Refs
• 降维方法
  • 降维动机
  • 方法
  • Refs
• 梯度消失问题缓解

梯度下降算法(优化器)

BGD&SGD

实现：https://gitee.com/Jonny-Jaia/ready-blog/blob/master/3-%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0/GradientDescent.py

批量梯度下降相当于直接对所有数据一次性梯度下降；

随机梯度下降则是在BGD的基础上增加随机打乱输入的数据；

Sharpness-Aware Minimization (SAM)

SAM:Sharpness-Aware Minimization for Efficiently Improving Generalization

研究背景

主要工作

1.

References

1. 不同梯度下降算法的比较及Python实现
2. Sharpness-Aware Minimization (SAM): 簡單有效地追求模型泛化能力
3. davda54/sam - Sharpness-Aware Minimization (PyTorch)

---

机器学习模型

线性函数与非线性函数的区别

通过增加非线性去拟合线性不可分的数据。如果不增加非线性操作，多层线性的操作链接等价于一层线性操作。

非线性函数使得映射更加复杂进而更容易拟合到对应的空间中去。

逻辑回归

Logistic Regression 虽然被称为回归，但其实际上是分类模型，并常用于二分类。

Logistic 回归的本质是：假设数据服从这个分布，然后使用极大似然估计做参数的估计。

逻辑回归是在线性回归的基础上加了一个 Sigmoid 函数（非线性）映射。

逻辑回归的思路是，先拟合决策边界(不局限于线性，还可以是多项式)，再建立这个边界与分类的概率联系，从而得到了二分类情况下的概率。

本质上来说，两者都属于广义线性模型，但他们两个要解决的问题不一样，逻辑回归解决的是分类问题，输出的是离散值，线性回归解决的是回归问题，输出的连续值。

优点

• 直接对分类的概率建模，无需实现假设数据分布，从而避免了假设分布不准确带来的问题（区别于生成式模型）；
• 不仅可预测出类别，还能得到该预测的概率，这对一些利用概率辅助决策的任务很有用；
• 对数几率函数（ Sigmoid 函数）是任意阶可导的凸函数，有许多数值优化算法都可以求出最优解。

代价函数

极大似然估计求解。在逻辑回归模型中，我们最大化似然函数和最小化损失函数实际上是等价的。

References

1. 【机器学习】逻辑回归（非常详细）

朴素贝叶斯分类器

References

1. 机器学习—朴素贝叶斯分类器（Machine Learning Naive Bayes Classifier） - HuZihu - 博客园 (cnblogs.com)

LSTM&GRU

LSTM:记忆单元+门控单元（遗忘门-sigmoid，会与旧的记忆相乘；输入门-分别用sigmoid和tanh调节输入-上一时刻隐特征+输入，加上上面的记忆单元；输出门-经过sigmoid，然后把记忆单元经过tanh在与其乘积得到输出）

LSTM避免梯度消失和梯度爆炸

一般梯度爆炸可以通过裁剪解决优化，针对梯度消失由于当前的状态是通过累加形式实现，不再是复合形式，使得梯度也不再是乘积的形式。进而解决梯度消失情况

GRU：

重置门&更新门

References

1. 25. 簡介LSTM 與GRU - Programming with Data - Medium

正则化

L1、L2正则化

L1范数：曼哈顿距离
L2范数：欧氏距离

数值理解

L1正则化是指权重矩阵中各个元素的绝对值之和，为了优化正则项，会减少参数的绝对值总和，所以L1正则化倾向于选择稀疏(sparse)权重矩阵（稀疏矩阵指的是很多元素都为0，只有少数元素为非零值的矩阵）。L1正则化主要用于挑选出重要的特征，并舍弃不重要的特征。

L2正则化是指权重矩阵中各个元素的平方和，为了优化正则项，会减少参数平方的总和，所以L2正则化倾向于选择值很小的权重参数（即权重衰减），主要用于防止模型过拟合。是最常用的正则化方法。一定程度上，L1也可以防止过拟合。

分布理解

我们可以分别假设权重的先验分布，进而得到当前的正则化效果，具体来说：

• L1正则化：先验分布-拉普拉斯分布
• L2正则化：先验分布-高斯分布

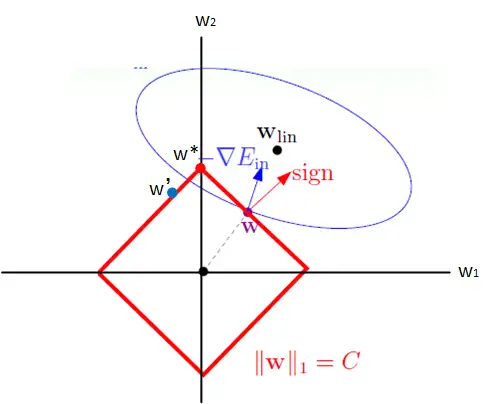
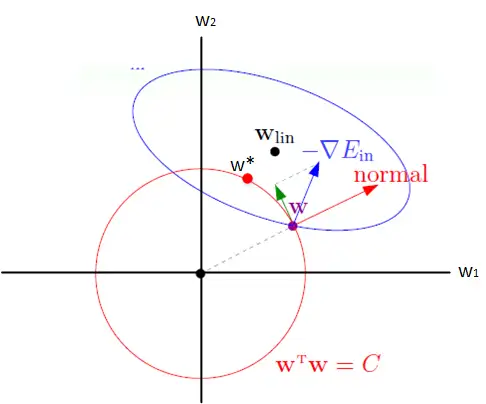
直观视觉

两种正则化就是在不同的范数球上更新权重

References

1. L1、L2正则化和过拟合
2. 深入理解L1、L2正则化

损失函数

分类问题用 Cross-entropy，回归问题用 mean squared error。

• 问题1：

均方差损失计算

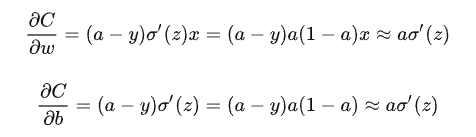
对于当前是逻辑回归算法的计算，当结果为0，1梯度都为0

当输入较大或者较少的时候会使得训练出现梯度消失的情况

交叉熵损失计算

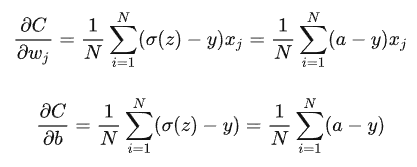
与均方差损失计算不同，就不会出现以上的情况

只取决于输出结果的偏差大小，梯度越大，训练速度越快

交叉熵

1. 二分类：
   $$ loss=-\frac{1}{N} \sum_{i=1}^{N} [y_i log(f(x_i)) + (1-y_i)log(1-f(x_i))] $$

2. 多分类：
   $$ loss=-\frac{1}{N} \sum_{k=1}^{N} \sum_{i=0}^{C-1}y_ilog(p_i) $$

交叉熵是用来评估当前训练得到的概率分布与真实分布的差异情况。 它刻画的是实际输出（概率）与期望输出（概率）的距离，也就是交叉熵的值越小，两个概率分布就越接近。

用交叉熵计算损失，当前问题依旧是凸优化问题。

优点：

• loss结果直接由误差控制优化

缺点：

• 采用了类内竞争机制

  只关心对于正确标签预测概率的准确性，忽略了其他非正确标签的差异，导致学习到的特征比较散。
  基于这个问题的优化有很多，比如对softmax进行改进，如L-Softmax、SM-Softmax、AM-Softmax等。

均方差损失(MSE)

$$ loss=\frac{1}{2}(y-\hat{y})^{2} $$

一个batch中n个样本的n个输出与期望输出的差的平方的平均值.

缺点：

• 当梯度比较小的时候，没办法判断当前是否在目标附近(很远的时候梯度也比较小)-梯度消失

KL散度

References

1. 【超详细公式推导】关于交叉熵损失函数（Cross-entropy）和 平方损失（MSE）的区别

Focal loss

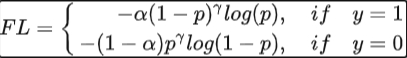
相当于当$\gamma=0$时，loss就是交叉熵带正负样本比例调节的版本。

GHM

Focal loss过于关注那些难分的样本也是有问题的，样本中存在离群点，过分关注反倒会使得性能下降。并且这一损失的计算由两个超参数同时调控，靠经验调优，是比较难实验得到好的效果的。

Refs

1. 5分钟理解Focal Loss与GHM——解决样本不平衡利器 - 知乎 (zhihu.com)

HMM与CRF

区别

• 类型：

CRF：判别模型，对问题的条件概率分布建模；

HMM：生成模型，对联合概率分布建模；

HMM可以看成是CRF的特殊情况。

• 特征选择：

CRF:可以用前一时刻和当前时刻的标签构成的特征函数，加上对应的权重来表示

HMM中的转移概率：可以用当前时刻的标签和当前时刻对应的词构成的特征函数，加上权重来表示 HMM 中的发射概率

• CRF的优势：

CRF 相比 HMM 能够利用更加丰富的标签分布信息

1. HMM只能使用局部特征，转移概率只依赖前一时刻和当前时刻，发射概率只依赖当前时刻，CRF 能使用更加全局的特征
2. HMM 中的概率具有一定的限制条件，如0到1之间、概率和为1等，而 CRF 中特征函数对应的权重大小没有限制，可以为任意值

判别式模型与生成式模型

1. 判别式

直接对$P(Y|X)$建模；对所有样本只构建一个模型，确认总体判别边界；对于输入的特征预测最有可能的label(在已知label里面挑选)；

优点：对数据量没有生成式严格，速度快，小数据量下准确率也会好些

2. 生成式

直接对$P(X,Y)$建模;要对每一个label都建模，选择最优概率label为结果；中间生成联合分布，可生成采样数据；包含信息十分齐全，因此需要比较充足的数据量，但速度相对更慢。

BiLSTM-CRF

CRF的引入

• 定义

在序列标注中，分别计算发射概率(x-yi)和转移概率(yi-1-yi),具体来说需要维护转移矩阵；

计算完得分之后，需要进行Normalizer计算-需要对当前x所有可能的输出序列得分计算求和，因此采用DP复用计算结果，提高效率。

解码过程，采用序列最优路径Viterbi算法。

beam search 的操作属于贪心算法思想，不一定reach到全局最优解。因为考虑到seq2seq的inference阶段的搜索空间过大而导致的搜索效率降低，所以即使是一个相对的局部优解在工程上也是可接受的。

viterbi属于动态规划思想，保证有最优解。viterbi应用到宽度较小的graph最优寻径是非常favorable的，毕竟，能reach到全局最优为何不用！

CRF矩阵的参数量

self.start_transitions = nn.Parameter(torch.empty(num_tags))
self.end_transitions = nn.Parameter(torch.empty(num_tags))
self.transitions = nn.Parameter(torch.empty(num_tags, num_tags))

CRF的更新

References

1. 概率图模型体系：HMM、MEMM、CRF
2. CRF 和 HMM 的区别与联系
3. CRF条件随机场的原理、例子、公式推导和应用
4. LSTM+CRF实现序列标注

常用的评价指标

分类任务：

1. 准确率：预测正确样本占样本的个数
2. 精确率：分类正确正样本占预测正样本个数
3. 召回率：分类正确正样本占真实正样本个数
4. P-R曲线：横轴召回、纵轴精确
5. F1：精确率与召回率的调和平均值
6. ROC曲线：横轴假阳性、纵轴真阳性
7. AUC：ROC曲线下的面积大小

回归任务：

1. 均方根误差

Refs

1. AUC、ROC详解：原理、特点&算法-腾讯云开发者社区-腾讯云 (tencent.com)
2. 模型评估指标AUC和ROC，这是我看到的最透彻的讲解-腾讯云开发者社区-腾讯云 (tencent.com)

归一化方法

将特征都归一化到大致相同的数值区间
使得算法更加稳定，加快算法的收敛速度
增加计算量、可能会导致信息丢失

机器学习：

1. 最大最小归一化
2. 线性归一化-直接除以最大值
3. 零均值归一化-减去均值除以方差:消除量纲的同时也消除各变量的差异(方差一致)

机器学习中的应用

需要归一化：KNN(需要计算距离)；线性回归、逻辑回归、SVM，NN(梯度下降求解，防止奇异值带来的影响)

不需要归一化：决策树、随机森林(树模型)-数值大小不影响条件概率以及对应的模型分裂点

深度学习：
尽可能保证输入的特征是独立同分布的，另外通过这种方式也能够降低结果在激活函数的非饱和区域出现梯度消失抑或是梯度爆炸等情况的出现。

1. batchnorm

对batch数据计算均值和方差。

问题：

• 一个batch里面的数据不能差异太大
• 由于batch的并行计算，不适用于动态网络结构和RNN网络(序列化数据网络)
• 适用于batch比较大，数据分布比较接近，且训练前经过充分的打乱
• 只用于训练不用于推理

2. layernorm

对样本单层输入做归一化处理，计算对应的均值和方差

• 避免受batch大小的影响
• 也可用于不同的场景
• 也不需要保存每个batch的均值和方差，节省存储

参考

1. 归一化方法总结 | 又名”BN和它的后浪们”
2. 【关于 归一化】那些你不知道的事
3. 【关于 BatchNorm vs LayerNorm】那些你不知道的事

多分类问题

机器学习中针对多分类问题，常用的解决办法就是训练多个分类器针对不同类别去分类。

可以直接是每个分类器针对单独类别进行识别；也可以是多个二分类器实现多分类的预测；

在深度学习中，其实可以直接设计多标签的形式进行模型训练，就不再采用softmax，采用binary_crossentropy损失函数函数。

高斯混合模型

Refs

1. 高斯混合模型 | 机器之心 (jiqizhixin.com)

降维方法

降维动机

1. 减少空间与训练用时，提高一些算法的可用性
2. 删除冗余特征，有助于可视化分析

方法

1. 删除

• 缺失值比率较高的
• 将低方差数据删除(说明数据基本一致，携带信息不足)
• 将相关度较高的变量删除（说明数据携带相似的信息）
• 采用随机森林选择小的特征子集
• 比较删除某变量之后的模型性能-反向特征消除
• 每次训练多个模型，将有性能提升的特征筛选出来

2. 新变量

• 因子分析-从多个变量中提取共性因子，将变量按照相关性分组，特定组内所有变量相关性较高，组间相关性低
• PCA
• 独立分量分析ICA-PCA寻找不相关的因素，而ICA寻找独立因素。
• 流形学习-解决非线性：UMAP、ISOMAP、t-SNE

Refs

1. 12种降维方法终极指南（含Python代码） - 知乎 (zhihu.com)

梯度消失问题缓解

GPT4

1. 使用ReLU激活函数：ReLU（Rectified Linear Unit）及其变种（如Leaky ReLU、Parametric ReLU和Exponential Linear Unit）是非饱和激活函数，它们在正区间内的梯度为1，因此不容易遭受梯度消失问题。

2. 使用更好的权重初始化方法：例如，使用He初始化或Glorot初始化可以帮助减少梯度消失或梯度爆炸问题。

3. 批量归一化（Batch Normalization）：批量归一化可以使每一层的输入都保持相同的尺度，从而减少梯度消失问题。

4. 使用残差网络（Residual Networks，ResNet）：ResNet通过引入跳跃连接（或称为残差连接）来避免梯度消失。这些连接允许梯度直接反向传播到较早的层。

5. 使用门控单元：在递归神经网络（RNN）中，使用长短时记忆网络（LSTM）或门控循环单元（GRU）可以帮助减少梯度消失问题。

6. 梯度剪裁（Gradient Clipping）：虽然这主要是为了避免梯度爆炸问题，但在某些情况下，它也可以帮助减少梯度消失。

7. 使用更浅的网络：减少网络的深度可以直接减少梯度消失问题，但这可能会牺牲模型的表示能力。

8. 使用其他优化器：某些优化器，如Adam、RMSprop等，已经内置了梯度的缩放机制，这可以在某种程度上减少梯度消失问题。

9. 正则化技术：如Dropout，虽然其主要目的是防止过拟合，但在某些情况下，它也可以帮助减少梯度消失。

10. 使用注意力机制：在序列到序列的模型中，使用注意力机制可以帮助模型关注输入序列的重要部分，从而减少梯度消失问题。