优化器
优化器
优化框架
概述:计算梯度之后的更新,需要考虑之前更新的一些情况,比如之前更新的幅度大小以及过去的更新累积。通过一阶动量的引入,减少梯度的震荡;通过二阶动量的引入,调控参数的更新频率,实现自适应的效果。最后,利用优化后的梯度量去更新参数。
- 计算目标函数对应的梯度:$g_t = \nabla f(w)$
- 根据历史梯度计算一阶动量与二阶动量 $m_t = \phi(g_1,g_2,..),V_t = \Phi(g_1,g_2,..)$
- 计算当前时刻的梯度下降大小:$\eta = \alpha \times m_t /\sqrt{V_t}$
- 参数更新:$w = w-\eta$
SGD
$m_t = g_t,\eta = \alpha \times g_t$
SGD with Momentum
为了抑制震荡,SGDM相当于加入了惯性,一阶动量$m_t = \beta_1 \cdot m_{t-1} + (1-\beta_1)\cdot g_t$
SGD with Nesterov Acceleration
防止提前陷入局部点,优化梯度计算,不采用当前位置的梯度方向,而是按照累积动量走了一步的下降方向进行更新。
$g_t = \nabla f(w_t-\alpha \cdot m_{t-1})$
AdaGrad
自适应学习率的第一次引入,借助二阶动量。由于经常更新的参数累积了大量的知识,我们不希望其会受到单个样本的影响过大,使得其学习率要小一些,而相反更新较少的参数则需要设置较大的学习率.
为了度量过去更新的频率,采用二阶动量-即是所有梯度值的平方和具体如下:
$V_t= \sum_{\tau=1}^{t}g_{\tau}^{2}$
那么梯度大小:
$\eta = \alpha \times m_t /\sqrt{V_t}$,其中分母会加上一个小值避免为0.
问题:由于二阶动量是递增的,会使得学习率单调递减至0,可能会使得训练提前结束。
AdaDelta/RMSProp
改进二阶动量的计算策略,不累积全部历史梯度,而只关注过去一段时间窗口的下降梯度。
新的二阶动量计算:
$V_t= \beta_2 \cdot V_{t-1} + (1-\beta_2)\cdot g_{t}^{2}$ 避免了二阶动量持续累积、导致训练过程提前结束的问题了。
Adam
Adam——Adaptive + Momentum-将一阶动量和二阶动量结合起来
SGD一阶动量$m_t = \beta_1 \cdot m_{t-1} + (1-\beta_1)\cdot g_t$
AdaDelta二阶动量$V_t= \beta_2 \cdot V_{t-1} + (1-\beta_2)\cdot g_{t}^{2}$
缺点:
- 当前这种窗口二阶动量会随着时间窗口变化,导致二阶动量时大时小,在训练后期会引起学习率的震荡导致模型无法收敛
修正:
$V_t= \max(\beta_2 \cdot V_{t-1} + (1-\beta_2)\cdot g_{t}^{2},V_{t-1})$ 保证学习率单调递减
- 自适应算法可能会对前期出现特征过拟合的情况,后期由于学习率太低等原因,会出现特征难以纠正前期的拟合效果,并最终影响收敛性能。
修正:
Adam+SGD
Nadam
Nesterov + Adam = Nadam
引入Nesterov 提前考虑下一步动作的梯度
$g_t = \nabla f(w_t-\alpha \cdot m_{t-1}/\sqrt{V_{t-1}})$
AdamW
AdamW就是Adam优化器加上L2正则
Ref
- 深度学习优化算法,从 SGD 到 AdamW 原理和代码解读
- 一个框架看懂优化算法之异同 SGD/AdaGrad/Adam - 知乎 (zhihu.com)
- Adam那么棒,为什么还对SGD念念不忘 (2)—— Adam的两宗罪 - 知乎 (zhihu.com)
- Adam那么棒,为什么还对SGD念念不忘 (3)—— 优化算法的选择与使用策略 - 知乎 (zhihu.com)
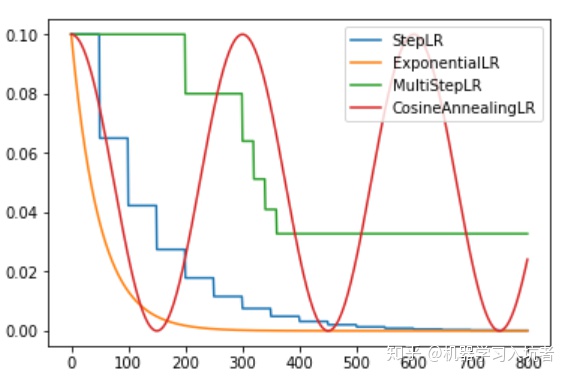
学习率衰减策略
字面意思直接控制学习率的变化